De Wikilibros, la colección de libros de texto de contenido libre.

[editar] Planos

Los planos son dibujos que representan las vistas de un objeto desde distintas posiciones. Tenemos planos de planta (vistos desde arriba),Planos de alzado (esp)o frente (arg) (vistos de frente),planos de perfil (esp) o Vistas (arg) (visto de costado),en realidad es como si tuviéramos un cubo , lo desplegáramos y todo que hay en esa cara esta representado en un plano. Tenemos planos de detalles (están a una escala mayor para apreciar mejor los detalles), planos de sección (esp o Corte (arg) (es cómo veríamos esa cara si le diéramos un corte imaginario) En construcción además tendremos planos de situación (esp) implantación (arg) (simplemente es un callejero en donde se indica el lugar donde ira la obra )

[editar] Planta de Replanteo (arg) Distribución (esp)

Este tipo de plano muestra como se vería el edificio desde arriba si se lo cortara a 1 metro del nivel del piso generalmente (este nivel puede variar según la necesidad de mostrar detalles del proyecto que se encuentren por encima de este nivel). Son los primeros planos de una obra, y permiten entender rápidamente como es la obra a grandes rasgos. Muestran la posición de las paredes, fundaciones, los ejes de replanteo, niveles, demás.

Primer ejemplo

Aquí mostraremos un ejemplo. Tomaremos el modelo de una casa muy simple y haremos su planta (no será una planta de replanteo completa pero será una primera aproximación)

1- se muestra la casa

2- se identifican los elementos que aparecerán en la planta

3- se de muestra en rojo la línea (imaginaria) de corte y por donde se cortará cada elemento (pared, puerta, ventanas)

4- se muestra la casa cortada

5- se muestra el plano resultante

Aquí mostramos el mismo plano, mas grande

En el plano de replanteo no se usan colores, el rojo solo lo usamos en la imagen anterior para mostrar el corte. En un plano de replanteo lo que se corta y lo que queda "de fondo" se diferencia con el espesor de línea, lo que se encuentra mas arriba (está mas cerca del observador) y se lo dibuja con líneas más gruesas, lo que esta mas abajo o tiene menos importancia se lo dibuja con líneas más finas.

Cosas a tener en cuenta de este primer plano:

-El dibujo de las ventanas: En las ventanas se corta el vidrio y el marco (que se dibujan con una línea gruesa), mientras que se puede ver mas lejos el antepecho (el pedazo de pared que está abajo).

-La puerta: Las puertas siempre se dibujan abiertas. Y se dibuja también una línea imaginaria que muestra el recorrido de la puerta al abrirse. Esta línea es imaginaria y de poca importancia, por eso se la dibuja finita. Lo importante de esta parte del dibujo es que nos indica para que lado debe abrir la puerta: Adentro o afuera, izquierda o derecha y si durante su recorrido afecta a elementos ubicados en el local, como un inodoro.

[editar] Escala

En un plano todas las medidas son proporcionales: es decir si la casa que va a construir tiene dos paredes y una es el doble de grande que la otra, en el plano será una del doble de largo que la otra. Si son las dos iguales, en el plano medirán lo mismo.

(agregar ejemplo)

Podemos decir que todos los elementos mantendrán una proporción entre sí, y por esto tendrán una proporción con la casa real. A esta proporción entre el dibujo y la realidad la llamamos escala.

Los planos de replanteo de obra suelen usar escalas de 1:50 o 1:100.

1:50 lo pronuncíamos "uno en cincuenta" y quiere decir que toda medida del plano es 50 veces mas chica que la realidad.

1:100 (uno en cien) quiere decir que todo es 100 veces mas chico, por lo que en el plano mide 1cm (centímetro) en la realidad mide 1m (metro)

Muchas personas no se sientes cómodas al tratar con los números y les cuesta entender el significado de la escala; pero interpretar una escala no exige necesariamente su traducción a unidades métricas para entenderla; es más sencillo: si un plano indica que su escala es 1:50 coloca sobre él, por ejemplo, un zapato, y la distancia que el zapato cubra sobre el plano significa que para cubrir esa misma distancia en la realidad necesitarás enfilar 50 zapatos como el utilizado.

[editar] Cotas

Por lo que acabamos de ver podríamos tomar todas las medidas de la obra midiendo con una regla o un escalímetro el dibujo. Sin embargo el plano de replanteo cuenta con un elemento gráfico (la cota) que marca una medida resumiendo el trabajo en obra y evitando posibles confusiones a la hora de necesitar una medida.

Existen tres tipos de cotas, las tres tienen el mismo fin, indicar medidas de objetos en el plano.

[editar] Cotas parciales

Miden una distancia dentro del plano: distancia entre paredes para conocer la medida de un local, distancia entre ejes de columna, distancia entre el filo de una carpintería y la parce mas cercana, etc.

Se dibujan como una línea cruzada por otras más pequeñas en los extremos que indican de donde a donde se está tomando la medida.

A continuación agregamos todas las cotas parciales a nuestro ejemplo. (atención, hemos girado el plano para que entrara mejor en la pantalla de su monitor.)

Este plano nos da la siguiente información.

-El local en el interior de la construcción mide 4,57m de largo y 2,88m de ancho.

-El ancho del local está acotado en la parte delantera como en la trasera para que en obra se corrobore que ambas paredes se mantengan paralelas.

-Los espesores de todas las paredes terminadas es de 17 cm (con revoques incluidos)

-El ancho de la puerta es de 90cm. Este ancho incluye al marco de la puerta.

-La distancia de la puerta esta acotada a ambos lados para verificar en obra que este bien ubicada. Además está acotada sola del lado interior por lo que es más importante su ubicación respecto del interior que del exterior. La puerta se encuentra a 1,69m del filo interior de la pared de la izquierda (izquierda para quien entra a la casa) y a 29 cm del filo interior de la pared de la derecha.

-La ventana pequeña (la del fondo) mide 65cm de ancho se encuentra a 68cm del filo exterior de la pared del fondo.

-La ventana grande mide 1,60m de ancho y se encuentra a 43cm del filo de la ventana pequeña. Aquí a diferencia de la puerta no se acotó a ambos lados porque no interesaba que las ventanas queden un poco más cerca o un poco más lejos del frente. Están acotadas del lado exterior porque importa más como se van a ver desde afuera que como van a quedar ubicadas dentro (en este caso).

-En una planta no se indican las alturas de ventanas y puertas ni su nivel de colocación

[editar] Cotas acumuladas

Estas cotas indican medidas más engorrosas de verificar en obra pero de gran importancia. Las cotas acumuladas indican la posición de cada elemento a construir dentro del terreno. Lo primero que se indica para esto son los ejes de replanteo. Los ejes de replanteo son dos líneas imaginarias que se ubican en el terreno. todas las cotas acumuladas que se presentas en la documentación serán distancias entre un punto que marque la cota y el eje correspondiente.

Los ejes de replanteo se los dibuja con una línea bien gruesa y con un trazo de "raya punto". Además se la reconoce porque se la indica con dos banderines cruzados en cada extremo.

En nuestro ejemplo ubicamos los ejes de replanteo de esta manera. Uno paralelo a la pared mas larga atravesará la puerta. Otro atravesará la ventana. Los dos ejes de replanteo son siempre perpendiculares entre sí, cuando las paredes de la casa conforman un ángulo recto.

Archivo:Cota acumulada replanteo2.jpg

A continuación marcamos los ejes de replanteo en nuestro ejemplo.

Archivo:Planta replanteo cotas acumuladas.jpg

Las cotas acumuladas se dibujan como flechas con el número que indica la distancia (magnitud) siempre expresas en metros de la siguiente manera 2.53 (2 metros, 53 centímetros). también son acompañadas de una letra que indican desde que eje se debe tomar la distancia.

Archivo:Cota de nivel.jpg

A continuación marcamos las cotas acumuladas

Archivo:Planta replanteo cotas de nivel.jpg

[editar] Cotas de nivel

Las cotas de nivel son un tipo de cota acumulada, pero en lugar de tomar distancias horizontales (largo de una pared), indica diferencia de altura (diferencia de altura entre un piso y otro). Para esto se indica en el plano cual es el nivel de referencia conocido como "el cero". A partir de este nivel las cotas iniciará +1.52 (una superficie que se encuentre 1metro y 52 centímetros más arriba que el cero) y -0.30 (una superficie que se encuentre 30 centímetros por debajo del nivel de referencia.

Las cotas de nivel se dibujan en la planta de replanteo como un círculo cruzado por una cruz con dos cuadrantes opuestos pintados y un número que indica la altura. El punto que mide es el que se encuentra justo en el centro del círculo.

A continuación marcamos las cotas de nivel sobre el plano indicado

[editar] Límite del terreno

Los límites del terreno se dibujan con una línea tipo "raya punto" o "raya punto punto" y un texto alineado que dice: "E.D.P." (eje divisorio de predios) o "L.M." (línea municipal). Sin embargo estas denominaciones varían en cada país.

En una planta es indispensable ubicar el límite del terreno para poder determinar la posición de todos los elementos de la obra.

Principalmente se acotan los ejes de replanteo al límite del terreno para luego ubicar cada elemento.

Así la ubicación en obra se hace de la siguiente manera:

• Se identifican los límites del terreno demarcados por el agrimensor.
• Se marcan los ejes de replanteo según su distancia a los límites del terreno.
• Se construyen los elementos principales (paredes, fundaciones, etc.) según su distancia a los ejes de replanteo (expresada en las cotas acumuladas)
• Se construyen los elementos secundarios (carpinterías, revestimientos, cielorrasos, etc) según su distancia a los elementos principales (expresada en las cotas parciales)

[editar] Proyecciones

Las proyecciones se dibujan con una línea de puntos e indican la presencia de elementos que están por encima de la línea de corte horizontal que determina la planta. Por ejemplo un balcón en el primer piso, se dibujará con una línea punteada su contorno en el plano de planta baja, indicando que allí arriba de nuestras cabezas existe un voladizo.

[editar] Pendiente

[editar] Corte

[editar] Plano detalle

(5c) Coordenadas

Las Coordenadas son grupos de números que describen una posición: posición a lo largo de una línea, en una superficie o en el espacio. La latitud y longitud o la declinación y ascensión recta, son sistemas de coordenadas en la superficie de una esfera: en el globo de la Tierra o en el globo de los cielos.    Coordenadas en el plano    René   Descartes El sistema más usado es de las coordenadas cartesianas, basado en un juego de ejes perpendiculares entre sí. Fue conocido con el nombre de René Descartes ("Dey-cart"), un científico y filósofo francés que, hacia el año 1600, ideó una forma sistemática de designar cada punto en el plano por medio de dos números. Puede que esto ya le sea familiar a usted. El sistema se basa en dos líneas rectas ("ejes"), perpendiculares entre sí, cada una marcada con las distancias desde el punto donde se juntan ("origen"): los espacios hacia la derecha del origen y hacia arriba de él, se toman como positivos y para los otros lados como negativos (vea el dibujo abajo).  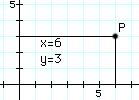La distancia en un eje se llama "x" y en el otro "y". Dado un punto P se dibujan, desde él, líneas paralelas a los ejes y los valores de "x" e "y" definen totalmente el punto. En honor a Descartes, esta forma de designación de los puntos se conoce como sistema cartesiano y los dos números (x, y) que definen la posición de cualquier punto son sus coordenadas cartesianas .  Las gráficas usan ese sistema, al igual que algunos mapas. 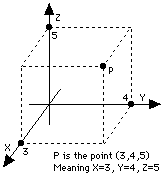 Funciona bien en una hoja de papel plana, pero el mundo real es tridimensional y a veces es necesario designar los puntos en dicho espacio tridimensional. El sistema cartesiano (x, y) puede extenderse hacia las tres dimensiones añadiendo una tercera coordenada z. Si (x, y) es un punto en una hoja, entonces el punto (x, y, z) en el espacio se consigue situándose en (x, y) y elevándose una distancia z sobre el papel (los puntos por debajo del papel tienen z negativa).  Es simple y claro, una vez que se toma la decisión de en qué lado de la hoja es positiva z. Por común acuerdo, las ramas positivas de los ejes (x, y, z), siguen el pulgar y los dos primeros dedos de la mano derecha, en el mismo orden, cuando se extienden de tal forma que formen el mayor ángulo entre ellos.  Lo que sigue usa las funciones trigonométricas seno y coseno. Si no está familiarizado con ellas, pase por alto esta sección o puede aprender sobre ellas. 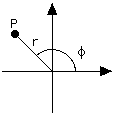Coordenadas Polares Las coordenadas cartesianas (x, y) no son la única forma de designar un punto P en el plano con un par de números. Existen otras formas y pueden ser más útiles en circunstancias especiales.  Un sistema (llamado de "coordenadas polares") usa la longitud r de la línea OP desde el origen hasta P y el ángulo que forma esa línea con el eje x. Los ángulos se denominan, a menudo, con letras griegas y aquí seguimos las convenciones designándolo como f (f griega). Observe que mientras en el sistema cartesiano x e y tiene roles muy similares, aquí están divididos: r denota la distancia y f la dirección. Las dos representaciones están muy relacionadas. De las definiciones de seno y coseno:  x = r cos f y = r sin f Esto permite que (x, y) se deduzcan de las coordenadas polares. Para ir en sentido inverso y deducir (r, f) de (x, y), observe que de las ecuaciones superiores o del teorema de Pitágoras se puede deducir r:  r2 = x2 + y2 Una vez que se conoce r, el resto es fácil  cos f = x/r  sin f = y/r  Estas relaciones solo fallan en el origen, donde x = y = r = 0. En ese punto, f está indefinido y se puede escoger para él lo que uno quiera.  En el espacio tridimensional, la designación cartesiana (x, y, z) es exactamente simétrica, pero algunas veces es conveniente seguir el sistema de coordenadas polares y designar la distancia y la dirección por separado. La distancia es fácil: se toma la línea OP desde el origen hasta el punto y se mide su distancia r. también puede deducirse del teorema de Pitágoras, como en este caso:  r2 = x2 + y2 + z2 Todos los puntos con el mismo valor de r forman una esfera de radio r alrededor del origen O. En una esfera se puede designar cada punto por la latitud l (lambda, l minúscula griega) y longitud f (phi, f minúscula griega), luego la posición de cualquier número en el espacio se define por 3 números (r, l, f).  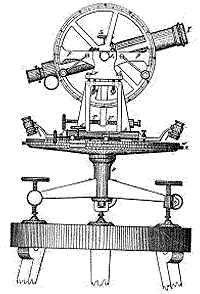Azimut y Elevación Un antiguo telescopio de topógrafo (teodolito). El teodolito está diseñado para medir esos ángulos. El ángulo f se mide en el plano horizontal, se le conoce como azimut y se mide desde la dirección norte. Una mesa giratoria permite al teodolito apuntar hacia cualquier azimut.  El ángulo l se llama elevación y es el ángulo con el que el teodolito se eleva sobre la horizontal (si mira hacia abajo, l es negativo). Los dos ángulos juntos pueden, en principio, especificar cualquier dirección: f tiene un rango de 0 a 360º, y l de -90º (perpendicular hacia abajo o "nadir") a +90º (perpendicular hacia arriba o "zenit").  De nuevo se necesita decidir desde qué dirección se mide el azimut, esto es, ¿donde está el azimut cero? La rotación de los cielos (y el hecho de que la mayoría de la humanidad vive al norte del ecuador), sugiere (para mediciones topográficas) la dirección norte, y esta es de hecho la dirección que se toma habitualmente como el punto cero. El ángulo del azimut (visto desde el norte) se mide en sentido antihorario.  Los matemáticos, no obstante, prefieren su propia notación y reemplazan "latitud" (o elevación) l, con colatitud q = 90 - l grados. No el ángulo con el horizonte, sino el ángulo con la vertical. El ángulo q (theta, una de las dos "tes" en griego) va de 0 a 180º, no de -90º a + 90º. Esto efectivamente puede tener más sentido, porque es más fácil medir un ángulo entre dos líneas (OP y la vertical) que entre la línea y el plano (OP y la horizontal).]  [Y por si usted necesita saberlo: Para referir (r, q, f) a las cartesianas (x, y, z) con el mismo origen, q se mide desde el eje z y f se mide en el plano (x, y), en sentido contrario a las agujas del reloj desde el eje x.]

CONSEJITOS

Si la anotación a la que te refieres es 1:25 que se lee 1 es a 25 y estas hablando de centímetros, entonces multiplicas 1x25 y te da la escala real en cms. . Y al revés si mides en la escala real por ejemplo de una habitación y en un lado te da 3 M, osea 300 cms estos los divides entre 25 y te da 12cm a escala 1:25 con la que puedes dibujar en tu plano a escal. las escalas 1:23 es igual solo multiplica o divide entre 23, e igualmente entre 100 en la escala 1:100. Ojo siempre debes de usar una sola escala en un mismo plano no mezclarlas y debes usar siempre las mismas unidades..Saludos desde León Gto. Méx.